Tutorial 5: Hyper-elasticity

Problem statement

using Gridap
using LineSearches: BackTracking

Material parameters

const λ = 100.0
const μ = 1.0

Deformation Gradient

F(∇u) = one(∇u) + ∇u'

J(F) = sqrt(det(C(F)))

#Green strain

#E(F) = 0.5*( F'*F - one(F) )

dE(∇du,∇u) = 0.5*( ∇du⋅F(∇u) + (∇du⋅F(∇u))' )

Right Cauchy-green deformation tensor

C(F) = (F')⋅F

Constitutive law (Neo hookean)

function S(∇u)
  Cinv = inv(C(F(∇u)))
  μ*(one(∇u)-Cinv) + λ*log(J(F(∇u)))*Cinv
end

function dS(∇du,∇u)
  Cinv = inv(C(F(∇u)))
  _dE = dE(∇du,∇u)
  λ*(Cinv⊙_dE)*Cinv + 2*(μ-λ*log(J(F(∇u))))*Cinv⋅_dE⋅(Cinv')
end

Cauchy stress tensor

σ(∇u) = (1.0/J(F(∇u)))*F(∇u)⋅S(∇u)⋅(F(∇u))'

Model

domain = (0,1,0,1)
partition = (20,20)
model = CartesianDiscreteModel(domain,partition)

Define new boundaries

labels = get_face_labeling(model)
add_tag_from_tags!(labels,"diri_0",[1,3,7])
add_tag_from_tags!(labels,"diri_1",[2,4,8])

Setup integration

degree = 2
Ω = Triangulation(model)
dΩ = Measure(Ω,degree)

Weak form

res(u,v) = ∫( (dE∘(∇(v),∇(u))) ⊙ (S∘∇(u)) )*dΩ

jac_mat(u,du,v) =  ∫( (dE∘(∇(v),∇(u))) ⊙ (dS∘(∇(du),∇(u))) )*dΩ

jac_geo(u,du,v) = ∫( ∇(v) ⊙ ( (S∘∇(u))⋅∇(du) ) )*dΩ

jac(u,du,v) = jac_mat(u,du,v) + jac_geo(u,du,v)

Construct the FEspace

reffe = ReferenceFE(lagrangian,VectorValue{2,Float64},1)
V = TestFESpace(model,reffe,conformity=:H1,dirichlet_tags = ["diri_0", "diri_1"])

Setup non-linear solver

nls = NLSolver(
  show_trace=true,
  method=:newton,
  linesearch=BackTracking())

solver = FESolver(nls)

function run(x0,disp_x,step,nsteps,cache)

  g0 = VectorValue(0.0,0.0)
  g1 = VectorValue(disp_x,0.0)
  U = TrialFESpace(V,[g0,g1])

  #FE problem
  op = FEOperator(res,jac,U,V)

  println("\n+++ Solving for disp_x $disp_x in step $step of $nsteps +++\n")

  uh = FEFunction(U,x0)

  uh, cache = solve!(uh,solver,op,cache)

  writevtk(Ω,"results_$(lpad(step,3,'0'))",cellfields=["uh"=>uh,"sigma"=>σ∘∇(uh)])

  return get_free_dof_values(uh), cache

end

function runs()

 disp_max = 0.75
 disp_inc = 0.02
 nsteps = ceil(Int,abs(disp_max)/disp_inc)

 x0 = zeros(Float64,num_free_dofs(V))

 cache = nothing
 for step in 1:nsteps
   disp_x = step * disp_max / nsteps
   x0, cache = run(x0,disp_x,step,nsteps,cache)
 end

end

#Do the work!
runs()

Picture of the last load step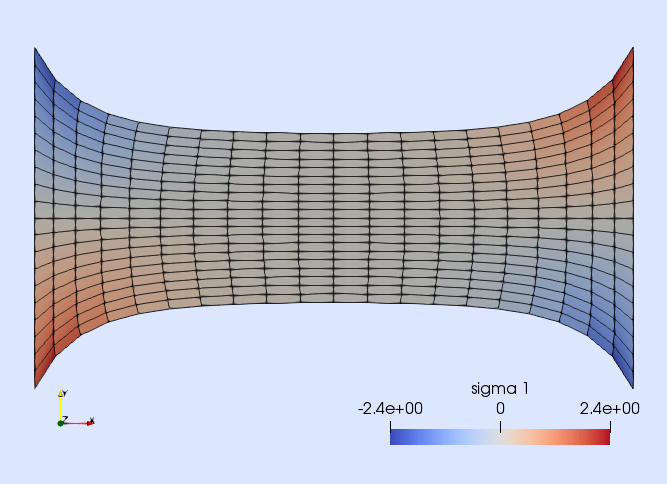

Extension to 3D

Extending this tutorial to the 3D case is straightforward. It is left as an exercise.

This page was generated using Literate.jl.